Following Hertz's experiments, the question
of the fundamental nature of light seemed clear: light consisted of em waves
that obeyed Maxwell’s theory. This certainty lasted only a dozen years. The
first sign that something was seriously a miss came from attempts to understand
the origin of the radiation emitted by bodies of matter.
We are all familiar with the glow of a hot
piece of metal, which gives off visible light whose color varies with the
temperature of the metal, going from red to yellow to white as it becomes
hotter and hotter. In fact, other frequencies to which our eyes do not respond
are present as well. An object need not be so hot that it is luminous for it to
be radiating em energy; all objects radiate such energy continuously whatever
their temperatures, though which frequencies predominate depends on the
temperature. At room temperature most of the radiation is in the infrared part
of the spectrum and hence is invisible.
The ability of a body to radiate is closely
related to its ability to absorb radiation. This is to be expected, since a
body at a constant temperature is in thermal equilibrium with its surroundings
and must absorb energy from them at the same rate as it emits energy. It is
convenient to consider as an ideal body one that absorbs all radiation incident
upon it, regardless of frequency. Such a
body is called a blackbody.
The point of introducing the idealized
blackbody in a discussion of thermal radiation is that we can now disregard the
precise nature of whatever is radiating, since all blackbodies behave
identically. In the laboratory a blackbody can be approximated by a hollow
object with a very small hole leading to Its interior (Fig. 2.5). Any radiation
striking the hole enters the cavity, where it is trapped by reflection back and
forth until it Is absorbed. The cavity walls are constantly emitting and
absorbing radiation, and it is in the properties of this radiation (blackbody
radiation) that we are interested.
Figure2.5 A hole in the wall of a hollow
object is an excellent approximation of a blackbody.
Experimentally we can sample blackbody
radiation simply by inspecting what emerges from the hole in the cavity. The
results agree with everyday experience. A blackbody radiates more when it is
hot than when it is cold, and the spectrum of a hot blackbody has its peak at a
higher frequency than the peak in the spectrum of a cooler one. We recall the
behavior of an iron bar as it is heated to progressively higher temperatures:
at first it glows dull red, then bright orange-red, and eventually it becomes
"white hot." The spectrum of blackbody radiation is shown in Fig.2.6
for two temperatures.
The color and brightness of an object heated
until it glows, such as the filament of this light bulb, depends upon its
temperature, which here is about 3000K. An object that glows white is hotter
than it is when it glows red, and it gives off more light as well.
Figure 2.6 Blackbody spectra. The spectral
distribution of energy in the radiation depends only or the temperature of the
body. The higher the temperature, the greater the amount of radiation and the
higher the frequency at which the maximum emission occurs. The dependence of
the latter frequency on temperature follows a formula called Wien's
displacement law, which is discussed in Sec.9.6.
THE ULTRAVIOLET CATASTROPHE
Why does the blackbody spectrum have the
shape shown in Fig.2.6? This problem was examined at the end of the nineteenth
century by Lord Rayleigh and James Jeans. The details of their calculation are
given in Chap.9. They started by considering the radiation inside a cavity of
absolute temperature T whose walls are perfect reflectors to be a series of
standing em waves (Fig. 2.7).
Figure2.7 Em radiation in a cavity whose
walls are perfect reflectors consists of standing waves that have nodes at the
walls, which restricts their possible wavelengths. Shown are three possible
wavelengths when the distance between opposite walls is L.
This is a three dimensional generalization
of standing waves in a stretched string. The condition for standing waves in
such a cavity is that the path length from wall to wall, whatever the
direction, must be a whole number of half-wavelengths, so that a node occurs at
each reflecting surface. The number of independent standing waves G(v)dv in the
frequency interval between v and dv per unit volume in the cavity turned out to
be
This formula is independent of the shape of
the cavity. As we would expect, the higher the frequency v, the shorter the
wavelength and the greater the number of possible standing waves.
The next step is to find the average energy
per standing wave. According to the theorem of equipartition of energy, a
mainstay of classical physics, the average energy per degree of freedom of an
entity (such as a molecule of an ideal gas) that is a member of a system of
such entities in thermal equilibrium at the temperature T is ½ kT.
Here k is Boltzmann's constant:
A degree of freedom is a mode of energy
possession. Thus a monatomic ideal gas molecule has three degrees of freedom,
corresponding to kinetic energy of motion in three independent directions, for
an average total energy of 3/2 kT.
A one-dimensional harmonic oscillator has
two degrees of freedom, one that corresponds to its kinetic energy and one that
corresponds to its potential energy. Because each standing wave in a cavity
originates in an oscillating electric charge in the cavity wall, two degrees of
freedom are associated with the wave and it should have an average energy of
2(1/2 kT):
The total energy u(v)dv per unit volume in
the cavity In the frequency interval from v to v+dv is therefore
This radiation rate is proportional to this
energy density for frequencies between v and v+dv. Equation (2.3), the
Rayleigh-Jeans formula, contains everything that classical physics can say
about the spectrum of blackbody radiation.
Even a glance at Eq.(2.3) shows that it
cannot possibly be correct. As the frequency v increases toward the ultraviolet
end of the spectrum, this formula predicts that the energy density should
increase as v2. In the limit of infinitely high frequencies, u(v)dv
therefore should also go to infinity. In reality, of course, the energy density
(and radiation rate) falls to 0 as v-->∞ (Fig. 2.8). This discrepancy became
known as the ultraviolet catastrophe of classical physics. Where did Rayleigh
and Jeans go wrong?
Figure 2.8 Comparison of the Rayleigh-Jeans
formula for the spectrum of the radiation from a blackbody at 1500K with the
observed spectrum. The discrepancy is known as the ultraviolet catastrophe
because it increases with increasing frequency. This failure of classical
physics led Planck to the discovery that radiation is emitted in quanta whose
energy is hv.
PLANCK RADIATION FORMULA
In 1900 the German physicist Max Planck used
"lucky guess work" (as he later called it) to come up with a formula
for the spectral energy density of blackbody radiation:
Here h is a constant whose value is
At high frequencies,
which means that u(v)dv-->0 as observed. No more ultraviolet catastrophe. At low frequencies, where the Rayleigh Jeans formula is a good approximation to the data (seeFig.2.8), hv << kT and hv/kT << 1. In general,
Thus at low frequencies Planck’s formula
becomes
Which is the Rayleigh-Jeans formula.
Planck's formula is clearly at least on the right track; in fact, it has turned
out to be completely correct.
Next Planck had the problem of justifying
Eq.(2.4) in terms of physical principles. A new principle seemed needed to
explain his formula, but what was it? After several weeks of "the most
strenuous work of my life, "Planck found the answer: The oscillators in
the cavity walls could not have a continuous distribution of possible energies ϵ
but must have only the
specific energies.,
An oscillator emits radiation of frequency v
when it drops from one energy state to the next lower one, and it jumps to the
next higher state when it absorbs radiation of frequency v. Each discrete
bundle of energy hv is called a quantum (plural quanta) from the Latin for
"how much."
With oscillator energies limited to nhv, the
average energy per oscillator in the cavity walls- and so per standing
wave-turned out to be not
as for a continuous distribution of oscillator energies, but
instead
This average energy leads to Eq.(2.4).
Blackbody radiation is further discussed in Chap.9.
Example
2.1
Assume that a certain 660-Hz tuning fork can
be considered as a harmonic oscillator whose vibrational energy is 0.04J.
Compare the energy quanta of this tuning fork with those of an atomic
oscillator that emits and absorbs orange light whose frequency is 5.00 X 1014
Hz.
Solution
(a) For the tuning fork,
The total energy of the vibrating tines of
the fork is therefore about 1029 times the quantum energy hv. The
quantization of energy in the tuning fork is obviously far too small to be
observed, and we are justified in regarding the fork as obeying classical
physics.
(b) For the atomic oscillator,
In electronvolts, the usual energy unit in
atomic physics, 3.32 X 10-19J
This is a significant amount of energy on an
atomic scale, and it is not surprising that classical physics fails to account
for phenomena on this scale.
The concept that the oscillators in the
cavity walls can interchange energy with standing waves in the cavity only in
quanta of hv is, from the point of view of classical physics, impossible to
understand. Planck regarded his quantum hypothesis as an "act of
desperation" and, along with other physicists of his time, was unsure of
how seriously to regard it as an element of physical reality. For many years he
held that, although the energy transfers between electric oscillators and em
waves apparently are quantized, em waves themselves behave in an entirely
classical way with a continuous range of possible energies.
Max
Planck (1858-1947) was born in Kiel and educated in Munich and Berlin. At the
University of Berlin he studied under Kirchhoff and Helmholtz, as Hertz had
done earlier. Planck realized that blackbody radiation was important because it
was a fundamental effect independent of atomic structure, which was still a
mystery in the late nineteenth century, and worked at understanding it for six
years before finding the formula the radiation obeyed. He "strived from
the day of its discovery to give it a real physical interpretation." The
result was the discovery that radiation is emitted in energy steps of hv.
Although this discovery, for which he received the Nobel Prize in 1918,is now considered to mark the
start of modern physics, Planck himself remained skeptical for along time of
the physical reality of quanta. As he later wrote, "My vain attempts to
somehow reconcile the elementary quantum with classical theory continued for many years and cost me
great effort....Now I know for certain that the quantum of action has a much
more fundamental significance than I originally suspected."
Like
many physicists, Planck was a competent musician (he sometimes played with
Einstein) and in addition enjoyed mountain climbing. Although Planck remained
in Germany during the Hitler era, he protested the Nazi treatment of Jewish
scientists and lost his presidency of the Kaiser Wilhelm Institute as a result.
In 1945 one of his sons was implicated in a plot to kill Hitler and was
executed. After World War II the Institute was renamed after Planck and he was
again its head until his death.











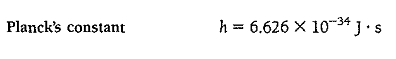










I'm looking for the first published plot comparing the Rayleigh-Jeans with observations and I can't find. Where did you get your figure 2.8? is that from a paper?
ReplyDelete