2.1 ELECTROMAGNETIC WAVES

Coupled electric and magnetic oscillations that move with the speed of light and exhibit typical wave behavior

In 1864 the British physicist James Clerk Maxwell made the remarkable suggestion that accelerated electric charges generate linked electric and magnetic disturbances that can travel indefinitely through space. If the charges oscillate periodically, the disturbances are waves whose electric and magnetic components are perpendicular to each other and to the direction of propagation, as in Fig.2.1.

 

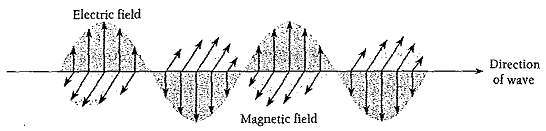
Figure 2.1 The electric and magnetic fields in an electromagnetic wave vary together. The fields are Perpendicular to each other and to the direction of propagation of the wave.

 

From the earlier work of Faraday, Maxwell knew that a changing magnetic field can induce a current in a wire loop. Thus a changing magnetic field is equivalent in its effects to an electric field. Maxwell proposed the converse: a changing electric field has a magnetic field associated with it. The electric fields produced by electromagnetic induction are easy to demonstrate because metals offer little resistance to the flow of charge. Even a weak field can lead to a measurable current in a metal. Weak magnetic fields are much harder to detect, however, and Maxwell's hypothesis was based on a symmetry argument rather than on experimental findings.

 

If Maxwell was right, electromagnetic (em) waves must occur in which constantly varying electric and magnetic fields are coupled together by both electromagnetic induction and the converse mechanism he proposed. Maxwell was able to show that the speed c of electromagnetic waves in free space is given by

 

 

Where ϵ_o is the electric permittivity of free space and μ_o is its magnetic permeability. This is the same as the speed of light waves. The correspondence was too great to be accidental, and Maxwell concluded that light consists of electromagnetic waves.

 

During Maxwell's lifetime the notion of em waves remained without direct experimental support. Finally, in1888, the German physicist Heinrich Hertz showed that em waves indeed exist and behave exactly as Maxwell had predicted. Hertz generated the waves by applying an alternating current to an air gap between two metal balls. The width of the gap was such that a spark occurred each time the current reached a peak. A wire loop with a small gap was the detector; em waves setup oscillations in the loop that produced sparks in the gap. Hertz determined the wavelength and speed of the waves he generated, showed that they have both electric and magnetic components, and found that they could be reflected, refracted, and diffracted.

 

Light is not the only example of an em wave. Although all such waves have the same fundamental nature, many features of their interaction with matter depend upon their frequencies. Light waves, which are em waves the eye responds to, span only a brief frequency interval, from about 4.3 X 10¹⁴ Hz for red light to about 7.5 X 10¹⁴ Hz for violet light. Figure2.2 shows the em wave spectrum from the low frequencies used in radio communication to the high frequencies found in x-rays and gamma rays.

 

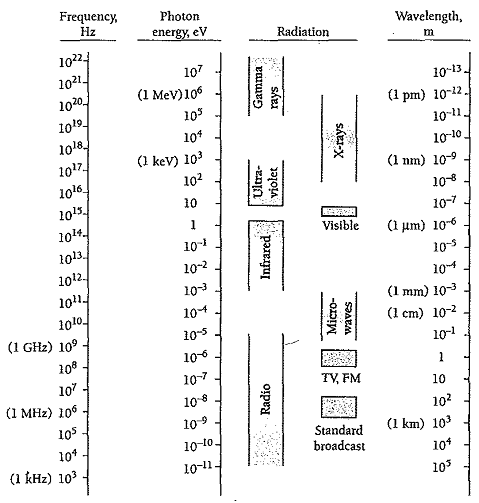
Figure2.2 The spectrum of electromagnetic radiation.

 

A characteristic property of all waves is that they obey the principle of superposition:

When two or more waves of the same nature travel past a point at the same time, the instantaneous amplitude there is the sum of the instantaneous amplitudes of the individual waves.

Instantaneous amplitude refers to the value at a certain place and time of the quantity whose variations constitute the wave. ("Amplitude" without qualification refers to the maximum value of the wave variable.) Thus the instantaneous amplitude of a wave in a stretched string is the displacement of the string from its normal position; that of a water wave is the height of the water surface relative to its normal level; that of a sound wave is the change in pressure relative to the normal pressure. Since the electric and magnetic fields in a light wave are related by E=cB, its instantaneous amplitude can be taken as either E or B. Usually E is used, since it is the electric fields of light waves whose interactions with matter give rise to nearly all common optical effects.

 

When two or more trains of light waves meet in a region, they interfere to produce a new wave there whose instantaneous amplitude is the sum of those of the original waves. Constructive interference refers to the reinforcement of waves with the same phase to produce a greater amplitude, and destructive interference refers to the partial or complete cancellation of waves whose phases differ (Fig 2.3). If the original waves have different frequencies, the result will be a mixture of constructive and destructive interference, as in Fig 3.4.

 

Figure2.3 (a) In constructive interference, superposed waves in phase reinforce each other. (b) In destructive interference, waves out of phase partially or completely cancel each other.

 

The interference of light waves was first demonstrated in 1801 by Thomas Young, who used a pair of slits illuminated by monochromatic light from a single source (Fig.2.4). From each slit secondary waves spread out as though originating at the slit; this is an example of diffraction, which, like interference, is a characteristic wave phenomenon. Owing to interference, the screen is not evenly lit but shows a pattern of alternate bright and dark lines. At those places on the screen where the path lengths from the two slits differ by an odd number of half wavelengths (λ/2, 3λ/2, 5λ/2,...), destructive interference occurs and a dark line is the result. At those places where the path lengths are equal or differ by a whole number of wavelengths (λ, 2λ, 3λ,...), constructive interference occurs and a bright line is the result. At intermediate places the interference is only partial, so the light intensity on the screen varies gradually between the bright and dark lines.

 

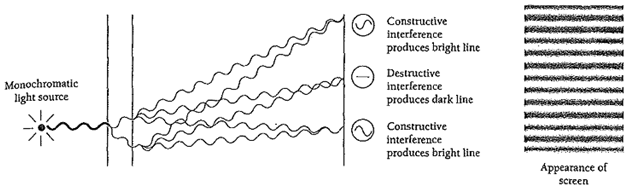
Figure 2.4 Origin of the interference pattern in Young's experiment. Constructive interference occurs where the difference in path from the slits to the screen is θ, λ, 2λ, .... Destructive interference occurs where the path difference is λ /2,3 λ /2,5 λ /2, ...

 

Interference and diffraction are found only in waves- the particles we are familiar with do not behave in those ways. If light consisted of a stream of classical particles, the entire screen would be dark. Thus Young's experiment is proof that light consists of waves. Maxwell’s theory further tells us what kind of waves they are: electromagnetic. Until the end of the nineteenth century the nature of light seemed settled forever.